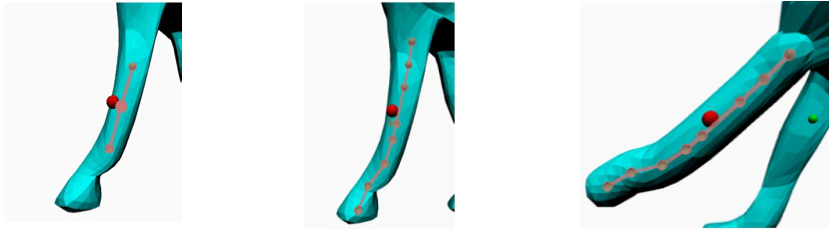
1. Tubular Mesh Generation
In this project, a program is developed to turn a cylinder-like mesh such as the horse leg shown in the figure below, into a tubular shape.
First, a propagational method is used to detect the median axis of the mesh, after finding the median axis, we can modify the vertexes on the mesh accordingly to generate a tubular shape.
First, a propagational method is used to detect the median axis of the mesh, after finding the median axis, we can modify the vertexes on the mesh accordingly to generate a tubular shape.
2. Skinning

In this project, a skinning algorithm is implemented to create a manifold mesh with a skeleton consists of spheres and cones.
My scheme of doing the skinning is to first sample the mesh with discrete points lying on the mesh. Using the sampling points, a manifold triangle mesh can then be constructed using ball-pivoting algorithm.
Since it is essential to generate a uniform sampling for the ball-pivoting algorithm, I developed two methods to generate uniform samplings for spheres and cones respectively.
The figure on the left is a screenshot of the generated mesh.
My scheme of doing the skinning is to first sample the mesh with discrete points lying on the mesh. Using the sampling points, a manifold triangle mesh can then be constructed using ball-pivoting algorithm.
Since it is essential to generate a uniform sampling for the ball-pivoting algorithm, I developed two methods to generate uniform samplings for spheres and cones respectively.
The figure on the left is a screenshot of the generated mesh.
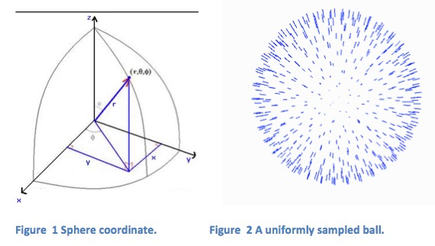
In the case of a sphere, I used a sphere coordinate where points on the sphere are represented by two angles, then a uniform sampling can be achieve by uniformly distribute one of the angles and then compute the corresponding value of the other. The sampling result is shown in 2.
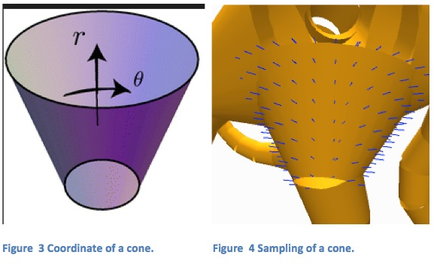
When the primitive is a cone, we can use a similar strategy as we did in the sphere, but this time a different coordinate is used. In stead of using two angles, we can use one angle and one length parameter to represent points on the cone. The sampling result is shown in figure 4.

After having a uniform sampling set, we can generate a mesh with the ball-pivoting algorithm. The basic idea is to simulate a ball rolling on the point cloud and each time the ball touches three points, we connect them into a triangle. The algorithm is given on the left and a more detailed description of it can be found in this paper.